Statistics Study Formula Sheet

(Not permitted during exams)

Topic Manual Formula         Excel Formula
Central Tendency:
Mean Sample:  Population:

=AVERAGE(first : last)
Weighted Mean 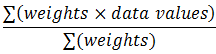Sum of the product of weights times data values over the sum of weights

 =SUMPRODUCT(weights, values) / n
Where n = SUM(weights)
Median If N is odd:  N plus 1, all divided by 2 If N is even:  N divided by 2 =MEDIAN(first : last)
Mode Data value with the most repeats.

 =MODE.SNGL(first : last)  or  =MODE.MULT(first : last)
Variability:
Range Maximum value minus minimum value.

 =MAX() - MIN()
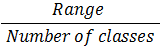
Class Width Range divided by number of classes. =range / number of classes
Variance Sample: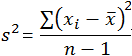 
Population: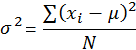


Sample: 
=VAR.S() 		Population:
=VAR.P()
Standard Deviation (SD) Sample: 

Population: 

Sample: 
=STDEV.S() 		Population: 
=STDEV.P()
Or,=SQRT(variance)
Or, =variance^0.5
Skewness 3 times (mean minus median), all divided by standard deviation.
 =3*(AVERAGE() - MEDIAN()) / SD
The above formula is used in our practice questions. There is an Excel skewness formula but answers are different:
=SKEW(first : last)
Excel internal skewness formula is:
Coefficient of Variation Sample: 
Population:
=SD / AVERAGE() * 100

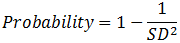Chebyshev		 Probability = 1 minus (1 divided by k squared).
Where k = number of standard deviations
= 1 - 1 / k^2
Where k = number of standard deviations
Grouped Data:
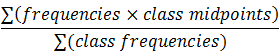Weighted Mean Sum of the product of frequencies times class midpoints over the sum of class frequencies
 =SUMPRODUCT(frequencies,class midpoints)/n
Where n = SUM(class frequencies)
Median Class that contains middle frequency:  N plus 1, all divided by 2
 class that has middle frequency: =(n+1)/2
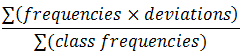Variance Sum of the product of frequencies times deviations over the sum of frequencies
Where deviations =(midpoint minus mean)squared, all divided by n.
Population is same except divide by n, instead of n-1.

 =SUMPRODUCT(frequencies,deviations)/(n-1)
Where deviations = (midpoint - mean)^2
Population is same except divide by n.
Standard Deviation

 Square root of variance.

 =SQRT(variance)
Position:
Percentile
Round up if decimal; average if whole.

 = percentile / 100 * n
Round up if decimal; average if whole.
IQR Interquartile Range = Q3 − Q1 = Q3 - Q1
Upper Outlier:  Q3 + 1.5(IQR)
 = Q3 + 1.5 * IQR
Lower Outlier:  Q1 − 1.5(IQR)

 = Q1 − 1.5 * IQR
Probability:
P(A) = A / Total
P(A or B) = P(A) + P(B) - P(A ∩ B)
same
same
Independent:
P(A and B) = P(A) × P(B) = P(A) * P(B)
Dependent:
P(A and B) = P(A) × P(B|A) = P(A) * P(B|A)
Conditional:
P(A | B) = P(A and B) / P(B) same
Bayes' Rule:
P(A | B) =       P(A|B)×P(B)      
P(A|B)P(B)+P(A|Bc)P(Bc)

= P(B|A)×P(A) / P(B)
=( P(A|B) * P(B) )  /  ( P(A|B)*P(B) + P(A|Bc)*P(Bc) )

= P(B|A) * P(A) / P(B)
Where or = union symbol.,   and = ∩,   given = |
Permutation

=PERMUT(n,r)

Where r = number of objects selected
Combination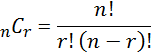

=COMBIN(n,r)
Discrete Distributions:
Expected Value =SUMPRODUCT(x,P(x))
Variance =SUM(x^2 * p) - (expected value^2))
Standard Deviation


=SQRT(Discrete Variance)
Binomial Distributions:
Mean

=n*p
Variance


=n*p*(1 - p)
Binomial Standard Deviation
=SQRT(n*p*(1-p))
Probability

 Probability of x equals n primed over x primed times ( n minus x ) primed all multiplied by p to the power of x times ( 1 minus p ) to the power of n minus x

 =BINOMDIST(successes,trials,probability,cum)
Normal Distributions:
Z Score Sample:   Population:   =(x - average()) / SD



Or,
=STANDARDIZE(x,mean,SD)
Z Score is the number of standard deviations between some value of x and the mean.
Z to Probability For manual calculations, look up probabilities in "Areas Under the One-Tailed Standard Normal Curve" table.

=NORM.S.DIST()
Less than:
=NORM.S.DIST(z score, 1)
More than:
=1-NORM.S.DIST(z score, 1)
Between:
=NORM.S.DIST(high z score,1) - NORM.S.DIST(low z score,1)
Probability Excel can calculate probability directly from X, Mean and Standard Deviation, but for manual calculations, compute z score and look up probability as described above. =NORM.DIST()
Less than:
=NORM.DIST(high value,Mean,SD,1)
Where the "1" means cumulative.
More than:
=1-NORM.DIST(low value,Mean,SD,1)
Between:
=NORM.DIST(high value,Mean,SD,1) - NORM.DIST(low value,Mean,SD,1)
Probability to Z Adjust probability (add or subtract .5).
Then look up the z closest to adjusted probability.

 =NORM.S.INV(Probability)
Probability to X x = z times standard deviation plus mean.
=NORM.INV(Probability,Mean,SD)
Sampling from Normal Distribution, Mean (Central Limit Theorem):
Standard Error Standard error = standard deviation divided by square root of n. Standard Error:
=SD / SQRT(n)
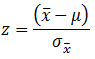
Probability 3 times (mean minus median), all divided by standard deviation. Less than:
=NORM.DIST(X,Mean,SD/SQRT(n),1)
Where 1 means cumulative.
More than:
=1-NORM.DIST(X,Mean,SD/SQRT(n), 1)
Between:
=NORM.DIST(high X,Mean,SD/SQRT(n),1) - NORM.DIST(low X,Mean,SD/SQRT(n),1)
Sampling from Normal Distribution, Proportion:
Validation If np greater than or equal to 5 and n(1 - p) greater or equal than 5.use the approximation for a normal probability distribution formula.
Where p = population proportion

 If n*p ≥ 5 and n*(1-p) ≥ 5 use:
Where p = population proportion
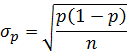
Standard Error The square root of (p times (1 minus p)), over n σp = SQRT(p*(1 - p) / n)
Z score Sample proportion minus population proportion, all divided by standard error for proportion. z = (ps - p) / σp
Probability Look up probabilities in "Areas Under the One-Tailed Standard Normal Curve" table.

 Less than:
NORM.S.DIST(z,1)
More than:
1-NORM.S.DIST(z,1)
Between:
=NORM.S.DIST(high z) - NORM.S.DIST(low z)
Confidence Intervals, Mean:
Alpha Alpha = 1 minus confidence level. Alpha = 1 - Confidence Level
Margin of Error E = z times standard deviation for x bar. =CONFIDENCE.NORM(alpha,SD,n)
Margin of Error Margin of error = t times standard error. (small sample)

 =CONFIDENCE.T(alpha,SD,n) (small sample)
Interval sample mean minus z score times standard error is less than or equal to the population mean which is less than or equal to the sample mean plus z score times standard error

 = (mean - E) to (mean + E)
Confidence Intervals, Proportion:
z Adjust probability (add or subtract .5) then look up z closest to adjusted probability.

 =NORM.S.INV(confidence level + alpha/2)
Margin of Error E = z times standard deviation for x bar.

 =z * SQRT(p * (1-p)/n)
Interval sample proportion minus z score times standard error is less than or equal to the population proportion which is less than or equal to the sample proportion plus z score times standard error

 =(proportion - E)  to  =(prop + E)
Sample Size, Mean:
(z value times standard deviation divided by allowed error) all squared

 =NORM.S.INV(confidence+Alpha/2)
Or:
=(z * SD / E)^2
Sample Size, Proportion:
Validation: np greater than or equal to 5 and n(1 - p) greater or equal than 5.
Population proportion times (1 minus population proportion) times the square of (z value divided by allowed error)

n*p ≥ 5 and n*(1-p) ≥ 5

p*(1 − p) * (z / E)^2

Hypothesis Tests:
Standard error: Test tatistic:
Mean 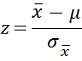Sample Standard Deviation divided by square root of sample size Sample mean minus population mean, all divided by standard error
1-tail: = NORM.S.INV(Confidence Level)
2-tail: = NORM.S.INV(Confidence Level + Alpha/2)
Test Statistic:
=(sample mean - mean) / (SD/SQRT(n))
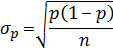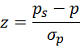Proportion The square root of (p times (1 minus p)), over n Sample proportion minus population proportion, all divided by standard error for proportion.

1-tail:  =NORM.S.INV(Confidence Level)
2-tail:  = NORM.S.INV(Confidence Level + Alpha/2)
Test Statistic:
=(ps - p) / SQRT(p*(1 - p) / n)
Small Sample 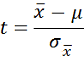Sample standard deviation divided by square root of sample size Sample mean minus population mean, all divided by standard error

1-tail: =T.INV(Alpha,df)
2-tail: =T.INV.2T(Alpha,df)
Where df = degrees of freedom = n - 1
P-Value 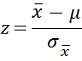Sample standard deviation divided by square root of sample size Sample mean minus population mean, all divided by standard error
1-tail:  z =NORM.DIST(sample mean, population mean, SD/SQRT(n),1)
2-tail:  z = NORM.DIST(sample mean, population mean, SD/SQRT(n),1) * 2
Regression Analysis:
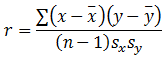Coefficient of Correlation: r = sum of (x minus x-bar bracket bracket y minus y-bar bracket, all over brachet n minus 1 bracket s sub x s sub y.
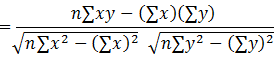
= n times the sum of xy minus bracket sum of x bracket bracket sum of y brachet, all over the root of n times the sum of x squared minus bracket sum of x bracket squared times the square root of n times the sum of y squared minus bracket sum of y bracket squared. 		In Excel statistics analysis:

"Multiple R"
Coefficient of Determination:    b = r squared. "R Square"
Regression Equation: y sub i = a plus bx.
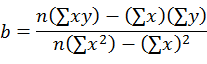Slope: b = (n(sum of x times y) minus (sum of x)(sum of y)) all divided by n(sum of x squared) minus (sum of x)squared.
 "X Variable" in Regression Statistics, or the heading you enter if you check "Labels" when you type data into Excel.
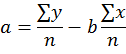Y Intercept:         a = sum of y divided by n minus b times the sum of x divided by n.
 "Intercept"
Standard Error Se 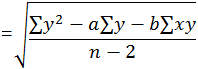= the square root of all of the following: the sum of y squared minus a times the sum of y minus b times the sum of xy, all divided by n minus 2.

 "Standard Error"
GrowingKnowing.com © 2010.   All rights reserved.


Formula Comparisons (for population data)

Univariate Discrete Binomial
Mean    

       
Variance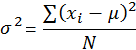    

       
Standard Deviation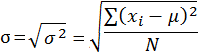                            

   GrowingKnowing.com © 2010.   All rights reserved.

Last updated:  September 20, 2023