Exam Statistics Formula Sheet, Manual

Mean Sample:  Population: 
Weighted Mean
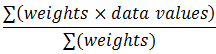Sum of the product of weights times data values over the sum of weights
Median If N is odd:   N plus 1, all divided by 2 If N is even:   N divided by 2
Mode Data value with the most repeats.
Range Maximum value minus minimum value.
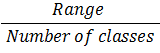
Class Width Range divided by number of classes.
Variance Sample: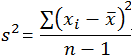 
 Population: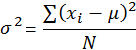 


Standard Deviation (SD)
Sample: 
 Population: 


Skewness 3 times (mean minus median), all divided by standard deviation.
Coefficient of Variation
Sample: 
 Population: 


Grouped Data Weighted Mean: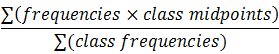
Sum of the product of frequencies times class midpoints over the sum of class frequencies
Median: Class with middle frequency:  N plus 1, all divided by 2
Variance:
Sum of the product of frequencies times deviations over the sum of frequencies
Where deviations =(midpoint minus mean)squared, all divided by n.
Population is same except divide by n, instead of n-1.

SD:  Square root of variance.
Chebyshev Probability = 1 minus (1 divided by k squared).
Where SD = number of standard deviations
Percentile
Round up if decimal; average if whole.
IQR, Outliers Interquartile Range = Q3 − Q1
Upper Outlier:  Q3 + 1.5(IQR)
Lower Outlier:  Q1 − 1.5(IQR)
Probability P(A) = A / Total
P(A or B) = P(A) + P(B) - P(A ∩ B)
Independent:
P(A and B) = P(A) × P(B)
Dependent:
P(A and B) = P(A) × P(B|A)
Conditional:
P(A | B) = P(A and B) / P(B)
Bayes' Rule:
P(A | B) =       P(A|B)×P(B)      
P(A|B)P(B)+P(A|Bc)P(Bc)

= P(B|A)×P(A) / P(B)
Where or = union symbol.,   and = ∩,   given = |
Permutation

Combination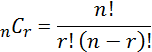

Discrete Distributions
Expected Value:


Variance:


SD:


Binomial Distributions
  Mean: 
  Variance:   Formula for binomial variance
  SD: 
  Probability:  Probability of x equals n primed over x primed times ( n minus x ) primed all multiplied by p to the power of x times ( 1 minus p ) to the power of n minus x
Normal Distributions
      Z Score: z = (X minus mean) divided by the standard deviation of the distribution.
Probability: Look up probabilities in "Areas Under the One-Tailed Standard Normal Curve" table.
Probability to Z:  Adjust probability (add or subtract .5) then look up z closest to adjusted probability.
Probability to X: 
x = z times standard deviation plus mean.
Sampling from Normal Distribution, Mean (Central Limit Theorem)
Standard Error:   Standard error = standard deviation divided by square root of n.
Probability:
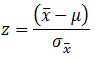3 times (mean minus median), all divided by standard deviation.
Sampling from Normal Distribution, Proportion
Validation:  np greater than or equal to 5 and n(1 - p) greater or equal than 5.
Standard Error: The square root of (p times (1 minus p)), over n
Z score: Sample proportion minus population proportion, all divided by standard error for proportion.
Probability:
Look up probabilities in "Areas Under the One-Tailed Standard Normal Curve" table.
Confidence Intervals, Mean
Alpha: Alpha = 1 minus confidence level.
Margin of Error:   E = z times standard deviation for x bar.
Margin of Error: 

Interval: 
Margin of error = t times standard error. (small sample)

sample mean minus z score times standard error is less than or equal to the population mean which is less than or equal to the sample mean plus z score times standard error
Confidence Intervals, Proportion
Margin of Error: 

Interval:  		E = z times standard deviation for x bar.
sample proportion minus z score times standard error is less than or equal to the population proportion which is less than or equal to the sample proportion plus z score times standard error
Sample Size, Mean
(z value times standard deviation divided by allowed error) all squared
Sample Size, Proportion
Validation:  np greater than or equal to 5 and n(1 - p) greater or equal than 5.
Population proportion times (1 minus population proportion) times the square of (z value divided by allowed error)

Hypothesis Tests   Standard Error: Test Statistic:
Mean: 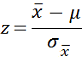Sample Standard Deviation divided by square root of sample size Sample mean minus population mean, all divided by standard error
Proportion: The square root of (p times (1 minus p)), over n Sample proportion minus population proportion, all divided by standard error for proportion.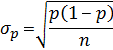
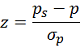Small Sample: 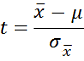Sample standard deviation divided by square root of sample size Sample mean minus population mean, all divided by standard error
P-Value: 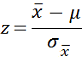Sample standard deviation divided by square root of sample size Sample mean minus population mean, all divided by standard error
Regression Analysis
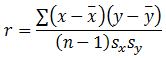
C. of Correlation: r = sum of (x minus x-bar bracket bracket y minus y-bar bracket, all over brachet n minus 1 bracket s sub x s sub y.
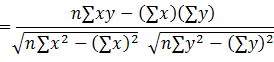
      = n times the sum of xy minus bracket sum of x bracket bracket sum of y brachet, all over the root of n times the sum of x squared minus bracket sum of x bracket squared times the square root of n times the sum of y squared minus bracket sum of y bracket squared.
C. of Determination: b = r squared.
Regression Equation: y sub i = a plus bx.
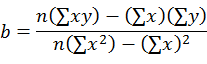Slope: b = (n(sum of x times y) minus (sum of x)(sum of y)) all divided by n(sum of x squared) minus (sum of x)squared.
Y Intercept: a = sum of y divided by n minus b times the sum of x divided by n.