Percentile

When to use it?

The percentile tells you the position among data values. If you scored a 90th percentile, what this concept says is that you beat 90% of the other people who took that test. A 30th percentile data value is higher than 30 out of every 100 data values. Percentile calculations are helpful when running a business. You may want to reward sales people who are above the 90th percentile, or you may drop products with sales profit below the 20th percentile.

Formula

The formula is:
Where "i" is the position within the ordered data of the value of "percentile".

If i is a decimal, round up, and the data value at position i in the SORTED data is the value at the given percentile.

If i is a whole number, take the data item in position i and average it with the data item in position i+1 in the SORTED data.

How to calculate a percentile?

In Excel, =Percentile(A1:A8, percentile)

Excel

=Percentile(A1:A9,0.3)
In this example you are looking for the 30th percentile in the data A1 to A9. Please note our general advice is do not use the Excel percentile function in Excel unless your teacher agrees.

By Hand

You must sort the data values first. Next, divide the percentile required by 100 and multiple by the number of data values. If you were asked for the 30th percentile, then find "i", using the formula: i = (30/100)n where:

n is the number of data values
i is the position of the percentile within the data

If i is a decimal number, round up to take the data value at that position. If i is a whole number, take the average of the data item in position i and i+1.

Caution - common mistakes?

Do not confuse 90 percent with 90 percentile. Percentile indicates position, but percent indicates value. Ninety percentile on a test means you got 9 out of every 10 questions correct. Ninety pcercentile means your mark was higher than 9 out of every 10 scores regardless of how many questions you got wrong. If most people failed the test, as long as your mark was higher than 9 out of 10 other students, you still scored 90th percentile despite your failure. If most people scored an A+ grade and you scored higher than 5 out of 10 of them, you are at 50 percentile with your A+ mark.

There are three popular methods to calculate a percentile and while there answers may agree, the answers are often different. For this reason, you should check with your insstructor to ensure the formula used is the same as Excel or the same shown here?

Percentile and Skewness are really the only statistics calculations in a first year college course where there are several different methods to calculate an answer depending on the textbook or teacher.

Examples

Find the 50th percentile given this data: 1, 4, 2, 5, 4.

Step 1:	Sort the data: 1, 2, 4, 4, 5
Step 2:	Calculate i = (percentile/100)n = (50/100)n = .5 × 5 = 2.5
Step 3:	i is a decimal therefore round up: i = 2.5, round up to 3, the third item is 4 so the 50th percentile is 4.

Find the 25th percentile given these numbers: 3,9,-1,0

Step 1:	Sort the numbers: -1, 0, 3, 9
Step 2:	Calculate i = (percentile/100)n = (25/100)4 = .25 × 4 = 1
Step 3:	i is a whole number therefore take the average of the two data values at positions i and i+1: i = 1 i+1 = 2 So, average the two data values at positions 1 and 2. Position 1 has -1 Position 2 has 0 The average of -1 and 0 is: (-1)+0/2 = (-1)/2 = -.5. Therefore, -0.5 is the 25th percentile.

Find the 25th percentile, given: 1, 3, 4, 4, 5

Step 1:	Using Excel, enter data into 5 cells, H1 through H5 in this example.
Step 2:	Insert Excel Percentile function using f_x: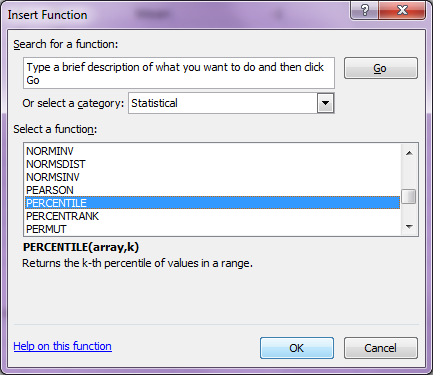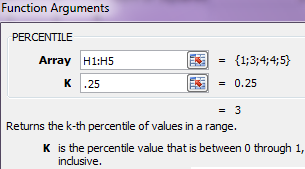
Step 3:	H6 shows the 25th percentile = 3 in this example:

Find the 50th percentile, given: -8, -5, 3, 9

Step 1:	Using Excel, enter data into 4 cells, J1 through J4 in this example.
Step 2:	Type Excel Percentile function into J5: